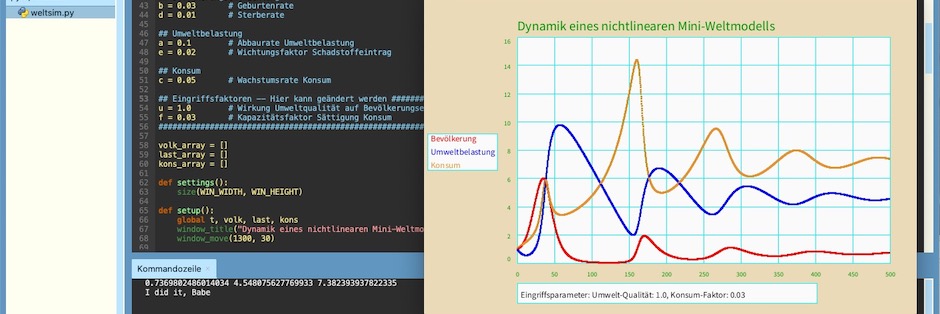
Dynamik eines nichtlinearen Mini-Weltmodells: Experimente mit Py5 und FPlotter

Nachdem ich vor ein paar Tagen meine »Matplotlib für Arme« FPlotter (2) von Processing.py nach Py5 portiert hatte, galt es, dies auch mit Leben zu erfüllen. Bevor ich damit die Ergebnisse der hier vorgestellten Waldbrandsimulation nach Al Sweigart visualisiere, wollte ich als Fingerübung erst einmal ein Modell von Hartmut Bossel, ein »nichtlineares Mini-Weltmodell«¹ in Py5 implementieren. Das erwies sich aufwendiger, als ursprünglich geplant, aber dafür kann sich das Ergebnis durchaus sehen lassen.

Ziel der Simulation ist es, ein (stark vereinfachtes) »Weltmodell« zu erstellen, das eine in etwa richtige Beschreibung der globalen Dynamik liefern kann, wie sie sich aus dem Zusammenspiel zwischen Bevölkerungsentwicklung, Umweltbelastung und Konsum entweickeln könnte. Dafür wird ein System aus drei gekoppelten Differentialgleichungen angenommen, die sich wie folgt zusammensetzen:

Die Bevölkerungsentwicklung (\(V\)) entspricht in etwa der Beziehung neue Bevölkerungszahl = alte alte Bevölkerungszahl + Geburtenrate (\(B\)) - Sterberate (\(D\)) (als Einheit wird – auch in allen folgenden Beziehungen/Gleichungen – ein Jahr vorausgesetzt). Das ergibt die Gleichung

\[ \frac{\Delta V}{\Delta t}=B-D \]

Im Teilmodell der Umweltbelastung (\(L\)) müssen zwei Verhaltensmöglichkeiten berücksichtigt werden. Liegt sie unter einem kritischen Wert (der Kapazitätsgrenze \(L^\ast\)), so ist der Abbau pro Zeiteinheit proportional zur vorhandenen Umweltbelastung. Liegt die Belastung dagegen über den kritischen Wert, so kann pro Zeiteinheit nur noch die (konstante) Menge abgebaut werden, die der Kapazitätsgrenze entspricht. Wenn die Belastung mit Schadstoffen pro Zeiteinheit gleich \(S\) ist und das Maß für die relative Umweltbelastung \(Q=\frac{L^\ast}{L}\), dann ergibt sich mit dem Parameter \(a\) für die spezifische Abbaurate folgende Gleichung:

\[ \frac{\Delta L}{\Delta t} = \begin{cases} S - a \cdot L & \text{ falls } L <= L^\ast \\ S - a \cdot L \cdot Q & \text{ falls } L > L^\ast \end{cases} \] Die Entwicklung des Konsums hingegen ist weitestgehend autokatalytisch, das heißt, es besteht eine positive Rückkoppelung zwischen dem Konsumniveau (\(K\)) und seiner Wachstumsrate. Das führt bei einer konstanten Wachstumsrate \(c\) zu exponentiellem Wachstum:

\[ \frac{\Delta K}{\Delta t} = c \cdot K \]

Da jedoch auch beim Konsumniveau exponentielles Wachstum zu einem Zusammenbruch des Gesamtsystems führen würde, wird also einer mehr oder weniger realistische Wachstumsbegrenzung angenommen. Sinnvoll ist die Annahme einer Kapazitätsgrenze \(K^\ast\) und der Modifizierung der Wachstumsrate so, daß diese sich bei der Annäherung an die Kapazitätsgrenze auf Null reduziert. Dies kann erreicht werden duch den logistischen Ansatz

\[ \frac{\Delta K}{\Delta t} = c \cdot K \cdot (1 - f \cdot K) \]

Dabei bestimmt der Kapazitätsfaktor \(f = \frac{1}{K^\ast}\), auf welchem Konsumniveau Sättigung eintritt.

Jetzt müssen diese Teilmodelle »nur« noch verkoppelt werden. Dabei trifft Bossel folgende Annahmen:

Die erste Verkopplung von Umweltbelastung (im Quellcode last) mit der Bevölkerungsentwicklung (im Quellcode volk) ist intendiert als Maßnahme zur Bevölkerungskontrolle in Reaktion auf hohe Umweltbelastung. Sie setzt daher bei der Geburtenrate an. Ausgangspunkt ist zweckmäßigerweise der bereits definierte Umweltqualitätsfaktor \(Q = \frac{L^\ast}{L} = \frac{1}{L}\). Bei sinkender Umweltqualität würde damit die Geburtenrate entsprechend verringert. Diese Wirkung ist durch den Faktor \(u\) zu beeinflussen².

Die zweite Kopplung von last nach volk beschreibt ein Sinken der Lebenserwartung durch den gesundheitsschädlichen Einfluß der Umweltbelastung. Sie muß deshalb von \(L\) auf die Sterberate wirken. Im Modell wird \(L\) direkt mit dem Faktor \(1\) für die Sterberate genutzt.

Die Kopplung von volknach last steht in einem direkten Zusammenhang mit der Kopplung des Konsums (im Quellcode kons) nach last, da der Schadstoffeintrag sowohl von der Bevölkerungsgröße wie auch von der Höhe des Konsums abhängt. Er ist daher proprtional zum Produkt \(V \cdot K\). Als Wichtungsfaktor wird im Modell \(e = 0.02\) eingesetzt.

Die Kopplung von kons nach volk modelliert die Erhöhung der Zahl der (überlebenden) Kinder bei wachsendem Wohlstand. Ähnlich wie bei der Verbindung von \(L\) auf die Sterberate wirkt \(K\) (ebenfalls mit der Gewichtung von \(1\)) direkt auf die Geburtenrate

Die Kopplung von kons nach volk nimmt an, daß eine Erhöhung der Umweltbelastung auch eine Erhöhung des Konsums mit sich zieht, daß \(L\) also auch auf die Wachstumsrate von \(K\) wirkt. Auch hier nimmt Bossels Modell wieder einen einfachen, proportionalen Einfluß mit der Gewichtung von \(1\) an.

Die letzte verbleibende Kopplung von last nach kons besitzt eine von der Eingriffsstärke abhängige Gewichtung, die bewirkt, daß das Wachstum des Konsumniveaus eine Grenze findet. Im Modell wird daher sinnvollerweise \(L\) mit dem Sättigungsterm so verkoppelt, daß auch diese Wichtung durch den Kapazitätsfaktor \(f\) ausgedrückt wird.

Unter diesen Annahmen erhalten wir ein Gleichungssystem, das aus folgenden, nichtlinearen Differentialgleichungen besteht:

\[ \begin{align*} \frac{\Delta V}{\Delta t} & = b \cdot V \cdot u \cdot (\frac{L^\ast}{L} K - d \cdot V \cdot L) \\ \frac{\Delta L}{\Delta t} & = \begin{cases} e \cdot K \cdot V - a \cdot L^\ast & \text{ falls } L > L^\ast \\ e \cdot K \cdot V - a \cdot L & \text{ falls } L <= L^\ast \end{cases} \\ \frac{\Delta K}{\Delta t} & = c \cdot K \cdot L \cdot (1 - K \cdot L \cdot f) \end{align*} \]

mit den Anfangsbedingungen

\[ V_0 = 1, L_0 = 1, K_0 = 1 \]

und den Paramtern

\[ a = 0.1, b = 0.03, c = 0.05, d = 0.01, e = 0.02 \]

Der Eingriffsparameter \(u\) sollte in der Nähe von \(1\) gewählt werden, der Eingriffsparameter \(f\) kann zwischen etwa \(0\) und \(10\) liegen.

In Code gegossen und mit Hilfe des Eulerschen Polygonzugverfahrens gelöst sieht das so aus:

def calc_world_model():
    global t, volk, last, kons
    qual = 1/last
    volk_rate = b*volk*u*qual*kons - d*volk*last
    if qual >= 1:
        abbau = a*last
    else:
        abbau = a*last*qual
    last_rate = e*kons*volk - abbau
    kons_rate = c*kons*last*(1 - (kons*last*f))
    # Numerische Lösung nach Euler
    volk = volk + volk_rate*dt
    last = last + last_rate*dt
    kons = kons + kons_rate*dt
    volk_array.append(volk)
    last_array.append(last)
    kons_array.append(kons)
    t += dt

Das der »Rest« des Skriptes mit insgesamt fast 200 Zeilen unerwarteterweise doch recht umfangreich geraten ist, liegt daran, daß mich das Bastelfieber gepackt hatte und ich die Plotfunktionen noch etwas aufhübschen wollte. Der Kasten links mit den Namen und Farben der einzelnen Kurven wie auch der Kasten unten mit den Eingriffsparamtern hatten etliche zusätzliche Codezeilen verursacht. Dafür ist das Gesamtergebnis (siehe Screenshot) doch recht nett geworden (wie ich als stolzer Schöpfer finde).

Nun aber – wie gewohnt – für alle, die gerne Quellcode lesen, das Skript nachvollziehen, nachprogrammieren oder variieren wollen, hier das komplette Programm:

# Einfache Simulation eines Weltmodells
# nach Hartmut Bossel: Modellbildung und Simulation
# Braunschweig 2. Auflage 1994, Seiten 78ff.

WIN_WIDTH, WIN_HEIGHT = 740, 480

# Plot-Parameter
plot_x1 = 140                    # Start Fensterbreite rechts
plot_x2 = WIN_WIDTH - 40         # Ende Fensterbreite links
label_x = 10
plot_y1 = 60                     # Start Fensterhöhe oben
plot_y2 = WIN_HEIGHT - 80        # Ende Fensterhöhe unten
label_y = WIN_HEIGHT - 35
plot_title = "Dynamik eines nichtlinearen Mini-Weltmodells"

## Sonstige Parameter
final = 500    # Simulationszeitraum (Jahre)
dt = 0.2       # Schrittweite

## Funktionsabhängige Konstanten
x_min = 0                        # Startwert x
x_max = final                    # Maximalwert x
y_min = 0                        # Startwert f(x)
y_max = 16                       # Maximalwert f(x)
stepsize_x = x_max//10           # Ticks auf der x-Achse
stepsize_y = -2                  # Ticks auf der y-Achse


# Farben
bg_color = color(234, 218, 184)           # Packpapier
text_color = color(0, 150, 0)             # Grün
text_color_2 = color(20, 20, 20)          # Schwarz
plot_window_color = color(250, 250, 250)  # Weiß
grid_color = color(0, 250, 250)           # Blau-Grau
line_color_1 = color(250, 0, 0)           # Rot
line_color_2 = color(0, 0, 250)           # Blau
line_color_3 = color(235, 146, 52)        # Orange


# Paramteter des Weltmodells

## Bevölkerungsentwicklung
b = 0.03       # Geburtenrate
d = 0.01       # Sterberate

## Umweltbelastung
a = 0.1        # Abbaurate Umweltbelastung
e = 0.02       # Wichtungsfaktor Schadstoffeintrag

## Konsum
c = 0.05       # Wachstumsrate Konsum

## Eingriffsfaktoren -- Hier kann geändert werden ###################
u = 1.0        # Wirkung Umweltqualität auf Bevölkerungsentwicklung #
f = 0.03       # Kapazitätsfaktor Sättigung Konsum                  #
#####################################################################

volk_array = []
last_array = []
kons_array = []

def settings():
    size(WIN_WIDTH, WIN_HEIGHT)

def setup():
    global t, volk, last, kons
    window_title("Dynamik eines nichtlinearen Mini-Weltmodells")
    window_move(1300, 30)

    ## Anfangswerte
    t = 1.0
    volk = 1.0     # Bevölkerungsentwicklung
    last = 1.0     # Umweltbelastung
    kons = 1.0     # Konsum
    
def draw():
    background(bg_color)
    draw_plot_window()
    calc_world_model()
    
    if t >= final:
        print(volk, last, kons)
        x = x_min
        i = 0
        while i < len(volk_array):
            stroke(line_color_1)
            x_v = remap(x, x_min, x_max, plot_x1, plot_x2)
            y_v = remap(volk_array[i], y_min, y_max, plot_y2, plot_y1)
            circle(x_v, y_v, 2)
            stroke(line_color_2)
            x_v = remap(x, x_min, x_max, plot_x1, plot_x2)
            y_v = remap(last_array[i], y_min, y_max, plot_y2, plot_y1)
            circle(x_v, y_v, 2)
            stroke(line_color_3)
            x_v = remap(x, x_min, x_max, plot_x1, plot_x2)
            y_v = remap(kons_array[i], y_min, y_max, plot_y2, plot_y1)
            circle(x_v, y_v, 2)
            x += dt
            i += 1
                                
        stroke(text_color)                       
        print("I did it, Babe")
        no_loop()
    

def calc_world_model():
    global t, volk, last, kons
    qual = 1/last
    volk_rate = b*volk*u*qual*kons - d*volk*last
    if qual >= 1:
        abbau = a*last
    else:
        abbau = a*last*qual
    last_rate = e*kons*volk - abbau
    kons_rate = c*kons*last*(1 - (kons*last*f))
    # Numerische Lösung nach Euler
    volk = volk + volk_rate*dt
    last = last + last_rate*dt
    kons = kons + kons_rate*dt
    volk_array.append(volk)
    last_array.append(last)
    kons_array.append(kons)
    t += dt
 
def draw_plot_window():
    # Den Plot in einem weißen Kasten zeichnen
    fill(plot_window_color)
    rect_mode(CORNERS)
    no_stroke()
    rect(plot_x1, plot_y1, plot_x2, plot_y2)
    # Kasten für y-Label
    stroke(grid_color)
    stroke_weight(1)
    rect(label_x - 5, (plot_y1 + plot_y2)//2 - 25, label_x + 100, (plot_y1 + plot_y2)//2 + 30)
    no_stroke()
    # Kasten für x-Label
    stroke(grid_color)
    stroke_weight(1)
    rect(plot_x1, label_y - 15, plot_x1 + 450, label_y + 15)
    no_stroke()
    # Titel des Plots zeichnen
    fill(text_color)
    text_size(20)
    text_align(LEFT)
    text(plot_title, plot_x1, plot_y1 - 10)
    draw_grid()
    draw_axis_labels()
    
def draw_grid():
    # Zeichne Gitter und Label
    text_size(10)
    text_align(CENTER, TOP)
    # x_Achse
    for i in range(x_min, x_max + 1, stepsize_x):
        x = remap(i, x_min, x_max, plot_x1, plot_x2)
        fill(text_color)
        text(str(i), x, plot_y2 + 10)
        stroke_weight(1)
        stroke(grid_color)
        line(x, plot_y1, x, plot_y2)
    # y-Achse
    for j in range(y_max, y_min - 1, stepsize_y):
        y = remap(j, y_max, y_min, plot_y1, plot_y2)
        if j == y_min:
            text_align(RIGHT, BOTTOM)   # Unten
        elif j == y_max:
            text_align(RIGHT, TOP)      # Open
        else:
            text_align(RIGHT, CENTER)   # Vertikal zentrieren
        fill(text_color)
        text(str(j), plot_x1 - 10, y)
        stroke_weight(1)
        stroke(grid_color)
        line(plot_x1, y, plot_x2, y)
        
def draw_axis_labels():
    text_size(13)
    text_leading(15)
    # y-Achse
    text_align(LEFT, CENTER)
    fill(line_color_1)
    text("Bevölkerung", label_x, (plot_y1 + plot_y2)//2 - 20)
    fill(line_color_2)
    text("Umweltbelastung", label_x, (plot_y1 + plot_y2)//2)
    fill(line_color_3)
    text("Konsum", label_x, (plot_y1 + plot_y2)//2 + 20)
    # x-Achse
    fill(text_color_2)
    text_size(13)
    text("Eingriffsparameter: Umwelt-Qualität: " + str(u) + ", Konsum-Faktor: " + str(f), plot_x1 + 5, label_y)
    fill(text_color)

Den Code findet Ihr natürlich auch in meinem GitHub-Repositorium.

Ein Wort noch zur Gültigkeit des Modells: Bossel selber weist darauf hin (S. 92f), daß sich sein Programm zwar im großen und ganzen plausibel verhält, daß dieser Eindruck aber nie dazu verleiten darf, den Modellergebnissen ohne weitere Überprüfungen bedingungslos zu vertrauen oder sie gar zur Grundlage wichtiger Entscheidungen zu machen. Vor allem müßte die empirische Gültigkeit und die Anwendungsgültigkeit hinterfragt werden.

Eine empirische Gültigkeit, das heißt eine zahlenmäßige Übereinstimmung mit der Realität, kann dieses Modell sicher nicht leisten. Dafür fehlen nicht nur die zahlenmäßigen Übereinstimmungen mit realen Größen mit meßbaren Entsprechungen im Realsystem, sondern auch die Parameter hätten wesentlich genauer (und komplexer) erfaßt und formuliert werden müssen.

Dagegen dürfte eine Anwendungsgültigkeit als einfaches, didaktisches Modell zur Demonstration der dynamischen Effekte elementarer Zusammenhänge zwischen Umwelt und der menschlichen Gesellschaft durchaus gegeben sein.

Diese Einschränkungen gelten aber nahezu für alle Modelle. So machen zum Beispiel Svein Linge und Hans Petter Langtangen in ihrem SIR-Modell zur Ausbreitung einer Grippe³ ähnliche Einschränkungen zur Güligkeit – und das, obwohl ihre Modellparameter eine viel kleinere Gruppe (Schüler in einem Internat) und nicht die ganze Welt, sondern nur einen begrenzten Raum (das Internat ist abgeschlossen von der Umwelt und besitzt daher keinen Kontakt zur Außenwelt) umfassen.

Behaltet diese Einschränkungen also im Hinterkopf, bevor Ihr in den sozialen Medien ein Faß aufmacht und über Wissenschaftlerinnen und Wissenschaftler im Besonderen und über Wissenschaft im Allgemeinen herzieht. Denn diese sind sich schon der Beschränkungen ihrer Modelle bewußt, aber die Presse, die die Ergebnisse vermitteln sollte, unterschlägt dies gerne und häufig.

Literatur

• Hartmut Bossel: Modellbildung und Simulation. Konzepte, Verfahren und Modelle zum Verhalten dynamischer Systeme. Ein Lehr- und Arbeitsbuch, Braunschweig (Vieweg) 2., veränderte Auflage mit verbesserter Simulationssoftware 1994
• Svein Linge, Hans Petter Langtangen: Programming Computations – Python. A Gentle Introduction to Numerical Simulations with Python 3.6, Cham CH (Springer) Second Edition 2020

Fußnoten

1. Vergleiche: Hartmut Bossel, Modellbildung und Simulation Braunschweig (Vieweg), 2. Auflage 1994, Seiten 78ff

2. Bossel nennt diesen Faktor \(g\), da aber g in Py5 ein »reservierter« Bezeichner ist, habe ich ihn in meiner Version durch \(u\) ersetzt.

3. Vergleiche: Svein Linge, Hans Petter Langtangen: Programming Computations, Cham CH (Springer) 2. Auflage 2020, Seiten 225ff