MicroStudio-Tutorial 5: PVector2 und »The Nature of Code« mit microStudio?

microStudio

Python

Brython

Nature of Code

Creative Coding

Spieleprogrammierung

Autor:in

Jörg Kantel

Veröffentlichungsdatum

28. März 2024

Je mehr und je länger ich mich mit microStudio in der Python/Brython-Variante beschäftige, um so mehr gelange ich zu der Überzeugung, daß sich das Teil für viel mehr eignet, als nur Spiele zu programmieren (obwohl auch das schon eine anspruchsvolle Aufgabe ist).

Mit der Nase darauf gestoßen wurde ich, als in meinen Feedreader die Videos »Vector motion with the math.Vector2« und »Rotating an image around its center with arctan2 and math.Vector2 gespült wurden¹. Sie behandeln die (relativ neue) Klasse math.Vector2 in Pygame:

Das rief Erinnerungen in mir wach: Ich hatte doch auch einmal – angelehnt an Processings PVector-Klasse eine 2D-Vector-Klasse in Pure-Python implementiert, die ich in der Nodebox, in der Arcade-Bibliothek (hier ein Beispiel), in TigerJython (auch ein Beispiel) und zuletzt in P5 (Python) (ein letztes Beispiel) eingesetzt hatte. Hinter all dem stand die Überlegung, Python-Versionen der Programme aus Daniel Shiffmans genialem Buch »The Nature of Code« (das dieses Jahr in einer lang erwarteten Neuauflage herauskommen soll) zu schaffen.

Und so kam in mir die Frage auf: Geht das nicht auch mit microStudio und Brython? Also habe ich ein altes Beispiel hervorgekramt und testweise im Rahmen meiner Tutorialreihe implementiert. Spoiler: Es geht!

Zuerst habe ich die Klasse Mover implementiert:

class Mover:
  
  def __init__(self):
    self.loc = PVector2(uniform(-screen.width//2, screen.width//2), uniform(-screen.height//2, screen.height//2))
    self.vel = PVector2(uniform(-5, 5), uniform(-5, 5))
    self.r = 15
    self.c = "rgba(255, 100, 255, 1.0)"
    self.stroke = "rgb(0, 0, 0)"
    
  def move(self):
    self.loc.add(self.vel)
    self.check_boundaries()
  
  def display(self):
    screen.fillRound(self.loc.x, self.loc.y, 2*self.r, 2*self.r, self.c)
    screen.drawRound(self.loc.x, self.loc.y, 2*self.r, 2*self.r, self.stroke)
  
  def check_boundaries(self):
    if self.loc.x >= screen.width//2 + 2*self.r:
      self.loc.x = -screen.width//2 - 2*self.r
    elif self.loc.x <= -screen.width//2 - 2*self.r:
      self.loc.x = screen.width//2 + 2*self.r
    if self.loc.y >= screen.height//2 + 2*self.r:
      self.loc.y = -screen.height//2 - 2*self.r
    elif self.loc.y <= -screen.height//2 -2*self.r:
      self.loc.y = screen.height//2 + 2*self.r

Hier habe ich ausgenutzt, daß microStudio – wie Ihr in der API-Dokumentation unter »Drawing Shapes« nachlesen könnt, eigentlich alle Methoden besitzt, um graphische Primitive wie Linien, Rechtecke, Kurven, Kreise und Ellipsen etc. zeichnen zu können. Um den Kreis mit einem Rand zu versehen, habe ich auf einen Trick zurückgegriffen: Ich zeichne erst mit fillRound() einen ausgefüllten Kreis und ziehe dann an der gleichen Stelle mit drawRound() noch einmal die Umrisse dieses Kreises nach.

Meine PVector-Klasse habe ich einfach aus meinem GitHub-Repositorium kopiert, lediglich den Namen habe ich – zur Verdeutlichung, das es sich um eine reine 2D-Implementierung handelt – in PVector2 geändert:

import math
import random

class PVector2():
    
  def __init__(self, x, y):
    self.x = x
    self.y = y

  def set(self, v):
    self.x = v.x
    self.y = v.y
    
  def get(self):
    v = PVector2(self.x, self.y)
    return v

  def add(self, v):
    self.x += v.x
    self.y += v.y
        
  def sub(self, v):
    self.x -= v.x
    self.y -= v.y
    
  # Multiplikation mit einem Skalar
  def mult(self, n):
    self.x *= n
    self.y *= n
    
  # Division durch einen Skalar
  def div(self, n):
    self.x /= n
    self.y /= n

  # Elementweise Multiplikation eines Vektor mit einem anderen Vektor
  def mult2(self, v):
    self.x *= v.x
    self.y *= v.y

  # Elementweise Division eines Vektor mit einem anderen Vektor
  def div2(self, v):
    self.x /= v.x
    self.y /= v.y

  # Magnitude
  def mag(self):
    return math.sqrt(self.x*self.x + self.y*self.y)
    
  # Normalisierung
  def normalize(self):
    m = self.mag()
    if (m != 0):
      self.div(m)

# Berechnung der euklidischen Distanz zwischen zwei Vektoren
  def dist(self, v):
    dx = self.x - v.x
    dy = self.y - v.y
    return math.sqrt(dx*dx + dy+dy)
    
  # Berechnung des Skalarprodukts (inneren Produkts) eines Vektors
  def dot(self, v):
    return self.x*v.x + self.y*v.y
    
  # Begrenzt die Magnitude eines Vektors auf max
  def limit(self, max):
    if self.mag() > max:
      self.normalize()
      self.mult(max)
    
  # Berechnet den Winkel der Rotation eines Vektors
  def heading(self):
    angle = math.atan2(-self.y, self.x)
    return -1*angle

  def __add__(self, other):
    x = self.x + other.x
    y = self.y + other.y
    result = PVector2(x, y)
    return result
    
  def __sub__(self, other):
    x = self.x - other.x
    y = self.y - other.y
    result = PVector2(x, y)
    return result
    
  def __str__(self):
    return "[" + str(self.x) + ", " + str(self.y) + "]"
        
  @classmethod
  def random2D(cls):
    x = random.uniform(-1, 1)
    y = random.uniform(-1, 1)
    v = cls(x, y)
    v.normalize()
    return v

  # Klassenmethoden: Skalare Multiplikation und Division
    
  # Multiplikation mit einem Skalar
  def smult(v, n):
    x = v.x*n
    y = v.y*n
    result = PVector2(x, y)
    return result

  # Division mit einem Skalar
  def sdiv(v, n):
    if n != 0:
      x = v.x/n
      y = v.y/n
      result = PVector2(x, y)
      return result
    else:
      print("Error. Divison durch Null!")

Das Hauptprogramm ist durch diese Modularisierung – so wie ich es liebe – wieder sehr übersichtlich geraten:

from random import uniform

def init():
  global mover
  mover = Mover()

def update():
  mover.move()

def draw():
  screen.fillRect(0, 0, screen.width, screen.height, "rgb(32, 62, 80)")
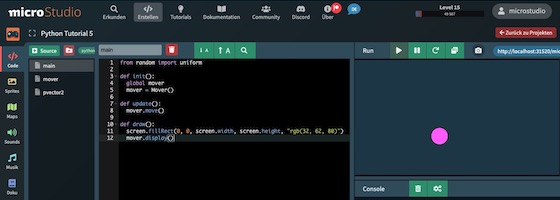
  mover.display()

Es passiert ja auch noch nicht viel: Nach jedem Neustart wird ein Kreis über den Bildschirm gejagt, der – wenn er die Grenzen des Fensters erreicht –, an der gegenüberliegenden Seite wieder auftaucht. Aber in diesem einfachen Beispiel liegt das große Versprechen, daß in microStudio und Python/Brython ein komplettes »Nature of Code« liegen könnte.

Und Vorsicht: Die PVector2-Klasse ist noch nicht wirklich ausgetestet. Ich werde mit ihr noch etliche Experimente durchführen müssen.

Damit ist die Liste meiner Tutorials zu microStudio mit Python um ein weiteres Element gewachsen:

MicroStudio und Python: Tutorial 1: Hallo Brython!
MicroStudio und Python (Teil 2): Zombie Apokalypse
MicroStudio und Python (Teil 3): Dancing Crab
MicroStudio und Python (Teil 4): Flying Badger
MicroStudio und Python (Teil 5): PVector2 und »The Nature of Code«

Auch dieses kleine Skript habe ich unter dem Titel »Python Tutorial 5« auf meinem microStudio-Account hochgeladen, damit Ihr damit spielen könnt. Und wer mir wirklich einen Gefallen tun will, der teste die PVector2-Klasse. Berichte in meinen Kommentaren sind willkommen.

Ich muß gestehen, so viel Spaß wie ich in den letzten Tagen mit microStudio und Python hatte, hatte ich schon lange nicht mehr. Still digging!

Fußnoten

Die Videos sind Teil einer Monsterplaylist »Game Programming«, bestehend aus (Stand heute) 66 Tutorials (das letzte Video ist vor fünf Tagen veröffentlicht worden, es kann also mit neuen Tutorials gerechnet werden). Und auch alle anderen Video-Tutorials des Kanals »DesignCodeDebugRepeat« (dahinter steckt die Autorin Margaret Burke) sind beachtenswert. Ich habe ihn daher abonniert.↩︎