Alice, die Grinsekatze und die Suche nach dem richtigen Weg

P5.js
Processing
Creative Coding
Autor:in

Jörg Kantel

Veröffentlichungsdatum

2. Juni 2024

»Grinse-Mieze,« fragte Alice die plötzlich erscheinende Grinsekatze, »willst du mir wohl sagen, wenn ich bitten darf, welchen Weg ich hier nehmen muß?«
»Das hängt zum guten Teil davon ab, wohin du gehen willst,« sagte die Katze.
»Es kommt mir nicht darauf an, wohin —« sagte Alice.
»Dann kommt es auch nicht darauf an, welchen Weg du nimmst,« sagte die Katze.
»— wenn ich nur irgendwo hinkomme,« fügte Alice als Erklärung hinzu.
»O, das wirst du ganz gewiß,« sagte die Katze, »wenn du nur lange genug gehst.«
(Lewis Caroll: Alice im Wunderland, Leipzig 1869)

Bei ihren Besuchen im Wunderland konnte sich Alice oft nicht entscheiden, ob sie die Teeparty des verrückten Hutmachers, das Haus der Herzogin oder die bekiffte Raupe auf ihrem Pilz besuchen solle. Alle drei Ziele lagen auf den Ecken eines Dreiecks. Doch wenn sie sich zum Beispiel entschloß, die Teeparty aufzusuchen, wurde sie genau auf der Hälfte des Weges unsicher. Sie ließ einen bunten Stein fallen und überdachte ihre Entscheidung noch einmal. Sie suchte also aus den drei möglichen Zielen zufällig eines aus (es konnte durchaus auch wieder die Party des verrückten Hutmachers sein). Doch es war wie verhext: Jedesmal, wenn sie genau den halben Weg zurückgelegt hatte, wurde sie wieder unschlüssig, ließ wieder einen bunten Stein fallen und überlegte neu, welches der drei möglichen Ziele (Hutmacher, Raupe oder Herzogin). sie aufsuchen sollte … möglicherweise das gleiche, möglicherweise ein anderes. Und das wieder, und wieder, und wieder …

Schaut man sich Alices Irrweg anhand der zurückgelassenen, bunten Steine an, entdeckt man eine Figur, genauer ein Fraktal, das in der Literatur als Sierpinski-Dreieck bekannt ist, benannt nach dem polnischen Mathematiker Wacław Sierpiński, der das Fraktal schon 1915 als erster beschrieb. Normalerweise wird dieses Fraktal mit einem rekursiven Algorithmus erzeugt, aber es geht eben auch mithilfe dieses »Chaos-Spiels«, das ich hier einmal in P5.js implementiert habe.

let i = 0;
let x = y = 0;

function setup() {
  createCanvas(600, 400);
  background(234, 218, 184);
  colorMode(HSB, 360, 100, 100);
  frameRate(120);
}

function draw() {
  let p = floor(random(0, 3));
  if (p == 0) {
    x /= 2;
    y = (y + height)/2;
  } else if (p == 1) {
    x = (x + width/2)/2;
    y /= 2;
  } else if (p == 2) {
    x = (x + width)/2;
    y = (y + height)/2
  }
  stroke(i%360, 100, 100);
  strokeWeight(2);
  point(x, y);
  i += 1;
  if (i > 24000) {
    print("I did it, Babe!");
    noLoop();
  }
}

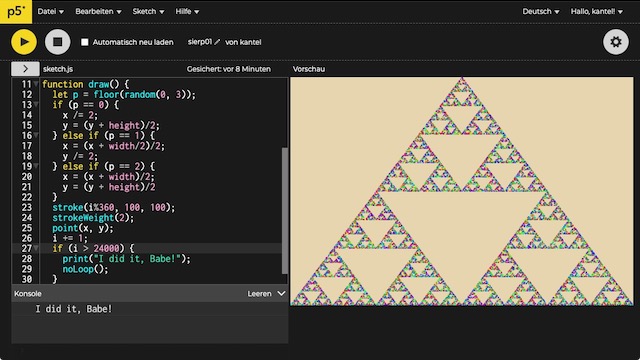
Die draw()-Schleife wird 24.000 Mal durchlaufen und obwohl ich die Framerate auf 120 FPS hochgetunt habe, müßt Ihr schon ein wenig Geduld aufbringen, bevor das erlösende »I did it, Babe!« in der Konsole erscheint. Aber man sieht sehr schön, wie sich das Dreieck zufällig, aber dennoch erkennbar, zusammensetzt. Je nach zufälligem Startwert liegen die ersten drei bis vier Punkte noch außerhalb des Fraktals, danach geht aber alles seinen geordneten Gang. Und an den Farben erkennt man, daß auch die Reihenfolge, in der die einzelnen Punkte des Fraktals von Alice angelaufen werden, ebenfalls zufällig sind.

Dieser Beitrag ist ein weiteres Puzzleteilchen für meine Tutorialreihe zu P5.js und läutet einen Abschnitt ein, der unter der Überschrift »Punkte und Pixel« steht. Und wie gewohnt, sind hier zum Schluß alle bisher erschienenen Tutorials aufgeführt, damit Ihr keine Suchmaschine Datenkrake bemühen müßt:

  1. Bouncing Faces: Drei Wege, mit P5.js zu spielen (GitHub)
  2. Luftballons im Wunderland: Erstes Abenteuer mit P5.js (GitHub)
  3. Der fliegende Dachs im Wunderland: Das Abenteuer P5.js geht weiter (GitHub)
  4. Abenteuer P5.js : Hallo Hörnchen! (GitHub)
  5. Abenteuer P5.js (Teil 5): Octopussy (GitHub)
  6. Das Abenteuer P5.js geht weiter: Ein kleines Planetensystem (GitHub)
  7. Rotating Images: Nachtrag zum Planetensystem mit P5.js (GitHub)
  8. Punkte und Pixel 1: Alice, die Grinsekatze und die Suche nach dem richtigen Weg (GitHub)

Literatur

  • William P. Beaumont: Conquering the Math Bogeyman, in Clifford A. Pickover (Ed.): Fractal Horizons – The Future Use of Fractals, New York (St. Martin’s Press) 1996, Seiten 3-15
  • Dietmar Herrmann: Algorithmen für Chaos und Fraktale, Bonn (Addison-Wesley) 1994, Seiten 132ff.

Update (3. Juni 2024)

Ich habe noch eine leicht modifizierte Version des Skriptes als P5.js-Widget eingebaut (ich habe die Canvasgröße und die Anzahl der Iterationen halbiert), damit Ihr da draußen etwas zum Spielen habt.

Bild: Alice und die Grinsekatze, Collage aus mehreren, KI-generierten Bildern.