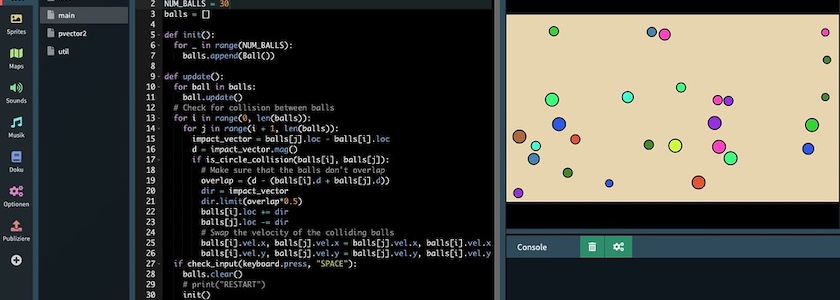
MicroStudio und Python: Bouncing Balls (ohne Überlappungen)

Mein Abenteuer »microStudio mit Python/Brython« geht weiter. Heute habe ich mich einem Problem gewidmet, das mich spätestens seit dem Beitrag »Bouncing Birds« verfolgt hat: Wenn ich eine Kollisionserkennung implementiert hatte, kam es in einigen Fällen vor, daß sich die Kreise überlappten und nur schwer wieder zu trennen waren. Das lag daran, daß – bedingt durch die Euler-Integration und die Framerate von 60 FPS – bei einer Kollision sich die Kreise so weit überschnitten, daß sie auch beim nächsten (oder über- (über-)) nächsten Schritt immer noch kollidierten.

Die Lösung ist aus der Spieleprogrammierung eigentlich bekannt: Bei einer Kollision setzt man die Akteure (die Kreise oder auch die Sprites) soweit auf die Position zurück, daß sie sich zwar gerade noch berühren, aber nicht mehr überlappen. Daniel Shiffman hat das in seiner 184. Coding Challenge »Collisions Without a Physics Library!« wunderbar erklärt. In microStudio/Brython sieht dann die Lösung so aus:

  # Check for collision between balls
  for i in range(0, len(balls)):
    for j in range(i + 1, len(balls)):
      impact_vector = balls[j].loc - balls[i].loc
      d = impact_vector.mag()
      if is_circle_collision(balls[i], balls[j]):
        # Make sure that the balls don't overlap
        overlap = (d - (balls[i].d + balls[j].d))
        diff = impact_vector
        diff.limit(overlap*0.5)
        balls[i].loc += diff 
        balls[j].loc -= diff 
        # Swap the velocity of the colliding balls
        balls[i].vel.x, balls[j].vel.x = balls[j].vel.x, balls[i].vel.x
        balls[i].vel.y, balls[j].vel.y = balls[j].vel.y, balls[i].vel.y

Wenn sich zwei Kreise überlappen, berechnet man zuerst den Abstand d und zieht davon die beiden Radii ab. Dann addiert man jeweils die Hälfte dieser Differenz diff auf die Position des einen Vektors und zieht beim zweiten Vektor die zweite Hälfte der Differenz ab. Dadurch werden beide Kreise auf eine Position gesetzt, die sich zwar gerade noch schneiden, aber nicht mehr überlappen. Als Kollisionsergebnis habe ich eine Reaktion gewählt, die von diesem Video »Python Bouncing Ball Simulator 5« von Christian Thompson (aka TokyoEdtech – Ihr wisst schon, der Mann, der Unglaubliches mit Pythons Turtle anstellt) inspiriert wurde: Bei einer Kollision wird einfach die Velocity der beiden beteiligten Kreise getauscht. Das ist zwar nicht wirklich eine exakte (ideale) elastische Kollision, kommt Ihr aber relativ nahe¹.

Das Ergebnis sieht dann so aus:

Für die Kollisionserkennung habe ich die Funktion is_circle_collision() wiederverwendet, die ich hier schon einmal eingeführt hatte und im Reiter util untergebracht:

def is_circle_collision(obj1, obj2):
  distance = math.dist([obj1.loc.x, obj1.loc.y], [obj2.loc.x, obj2.loc.y])
  if distance < obj1.d + obj2.d:
    return True
  return False

Wenn man mal von der Kollisionsbehandlung absieht, wird die meiste Arbeit in der Klasse Ball erledigt, die so aussieht:

from random import randint, choice

colors = ["rgba(230, 96, 55, 200)", "rgba(17, 42, 106, 200)",
          "rgba(183, 116, 64, 200)", "rgba(212, 251, 69, 200)",
          "rgba(252, 75, 200, 200)", "rgba(159, 53, 233, 200)",
          "rgba(57, 218, 56, 200)", "rgba(67, 253, 133, 200)",
          "rgba(78, 148, 42, 200)", "rgba(67, 254, 211, 200)",
          "rgba(74, 143, 186, 200)", "rgba(52, 99, 234, 200)"]
          
class Ball:
  
  def __init__(self):
    self.d = randint(4, 7)   # randint(4, 10)
    self.w, self.h = self.d*2, self.d*2
    x = randint(int(-screen.width//2 + self.d),
                int(screen.width//2 - self.d))
    y = randint(50, 100)
    self.loc = PVector2(x, y)
    dx = randint(-3, 3)
    dy = 0
    self.vel = PVector2(dx, dy)
    self.gravity = 0.01
    self.c = choice(colors)
    self.stroke = "rgb(0, 0, 0)"

  def update(self):
    self.vel.y -= self.gravity
    self.loc.add(self.vel)
    # check border
    if self.loc.y <= -screen.height//2 + self.d:
      self.loc.y = -screen.height//2 + self.d
      self.vel.y *=-1
    if self.loc.x <= -screen.width//2 + self.d:
      self.loc.x = -screen.width//2 + self.d
      self.vel.x *= -1
    if self.loc.x >= screen.width//2 - self.d:
      self.loc.x = screen.width//2 - self.d
      self.vel.x *= -1
      
  def draw(self):
    screen.fillRound(self.loc.x, self.loc.y, self.w, self.h, self.c)
    screen.drawRound(self.loc.x, self.loc.y, self.w, self.h, self.stroke)

Die Bewegung der Kreise wird vertikal (in y-Richtung) von einer Gravitationskraft gravity beeinflusst, die von der Velocity abgezogen wird. Kollidiert der Kreis mit dem unteren Fensterrand, wird das Vorzeichen umgekehrt, der Kreis steigt wieder nach oben, bis wieder soviel zum negativen Wert hinzuaddiert ist, daß die Velocity wieder positiv wird und sie wieder nach unten fällt. Die horizontale Richtung (x-Achse) wird von einer Konstanten gesteuert, die per Zufallszahlengenerator zwischen -3 und 3 erzeugt wird. Ihr seid eingeladen, mit diesen Werten zu spielen.

Aber auch bei der Behandlung der Ränder (Boden, Seitenwände) bin ich dieses Mal genauer. Wenn der Wert kleiner oder gleich der Position des Bodens oder der Seitenwände ist, wird er exakt auf die Position des Bodens oder der Seitenwände gesetzt².

Die Hauptroutine ist – bis auf die Zeilen zur Kollisionserkennung, die ich aber auch in die Klasse Ball hätte auslagern können – wieder recht kompakt geraten:

import math
NUM_BALLS = 30
balls = []

def init():
  for _ in range(NUM_BALLS):
    balls.append(Ball())

def update():
  for ball in balls:
    ball.update()
  # Check for collision between balls
  for i in range(0, len(balls)):
    for j in range(i + 1, len(balls)):
      impact_vector = balls[j].loc - balls[i].loc
      d = impact_vector.mag()
      if is_circle_collision(balls[i], balls[j]):
        # Make sure that the balls don't overlap
        overlap = (d - (balls[i].d + balls[j].d))
        diff = impact_vector
        diff.limit(overlap*0.5)
        balls[i].loc += diff 
        balls[j].loc -= diff 
        # Swap the velocity of the colliding balls
        balls[i].vel.x, balls[j].vel.x = balls[j].vel.x, balls[i].vel.x
        balls[i].vel.y, balls[j].vel.y = balls[j].vel.y, balls[i].vel.y
  if check_input(keyboard.press, "SPACE"):
    balls.clear()
    # print("RESTART")
    init()

def draw():
  screen.clear("rgb(234, 218, 184)")
  for ball in balls:
    ball.draw()

Ihr habt hoffentlich bemerkt, daß durch die Einführung der Liste balls[] und der Klasse Ball die von mir nicht geliebte Deklaration von ball als global weggefallen ist.

Wie immer habe ich auch dieses Skript auf meinen microStudio-Account hochgeladen. Macht damit, was Ihr wollt.

Literatur

Bei der Programmierung und zur Vertiefung des Beitrags haben mir folgende Texte und Videos geholfen:

1. Daniel Shiffman: Collisions Without a Physics Library! (Coding Challenge 184) vom 13. Juli 2024
2. Christan Thompson (aka TokyoEdtech): Bouncing Ball Simulator, Playlist mit fünf Videos, zuletzt aktualisiert am 3. November 2020
3. Reducible: Building Collision Simulations: An Introduction to Computer Graphics, Video-Tutorial vom 19. Januar 2021
4. Wikipedia-Artikel: Stoß (Physik), zuletzt besucht am 19. März 2025
5. Chad Berchek: 2-Dimensional Elastic Collisions without Trigonometry (PDF), 3. August 2009

Alle bisherigen Beiträge zu Microstudio und Python/Brython im Schockwellenreiter

• MicroStudio und Python (Teil 1): Hallo Brython!
• MicroStudio und Python (Teil 2): Zombie Apokalypse
• MicroStudio und Python (Teil 3): Dancing Crab
• MicroStudio und Python (Teil 4): Flying Badger
• MicroStudio und Python (Teil 5): PVector2 und »The Nature of Code«
• MicroStudio und Python (Teil 6): Bouncing Balls
• MicroStudio und Python (Teil 7): Kollisionserkennung mit Kreisen
• MicroStudio und Python (Teil 8): Bouncing Birds
• MicroStudio und Python (Teil 9): Kollisionserkennung mit Rechtecken
• MicroStudio und Python (Teil 10): Bubbly Emojis
• MicroStudio und Python (Teil 11): Ein Partikelsystem
• MicroStudio und Python (Teil 12): Ein Partikelsystem (2)
• MicroStudio und Python (Teil 13): Bouncing Duck (mit Vektoren)
• MicroStudio und Python (Teil 14): Bouncing Balls (ohne Überlappungen)

Mit der (Wieder-) Entdeckung von microStudio mit Python/Brython hatte ich bisher viel Spaß. Schauen wir mal, was die Zukunft mir noch bringen wird. Still digging!

Fußnoten

1. Wer eine genauere Simulation einer elastischen Kollision (eines (in diesem Falle zweidimensionalen) elastischen Stoß) implementieren will, kann sich ja an Shiffmans Implementierung orientieren. Oder sie oder er greifen gleich zu einer Physik Engine (microStudio will ja auch in Brython mit Matter.js zusammenspielen).

2. Dadurch werden auch hier mögliche Glitches beseitigt, die von der Euler-Integration und der Framerate von (maximal) 60 FPS hervorgerufen werden könnten.